以前学线代是为了应试,做题相当溜,理解一抹黑。恰似阿尔法狗下围棋,下得人类莫敢撄锋,但其实狗眼看棋全比特——就没抽象出围棋这概念。正好过年有大把时间,可以干一些早就有兴趣干的事,比如打开某个尘封已久的收藏夹。
本文大框架来源于 3Blue1Brown 的线代系列课程,其中替换了很多个人的理解方式和零碎的网络片段。撰写本文的主要目的是想通过亲手再加工以加深理解,写完发现诸位网友诚不欺我,因为我越写越发现只看不写得来的理解浑身都是窟窿。
线性空间
- 线性空间的一组基定义:张成该空间的一个线形无关向量的集合。
- 规范正交基定义:彼此正交的一组单位向量。本文中设二维线性空间的一组规范正交基为 $\vec{i},\vec{j}$。
- 理解基向量:
- 每个基向量都给张成的空间增添了一个新的维度。
- 我初次接触基向量这个概念时,下意识地认为这个名称描述的一定是个独一无二的玩意,八成仅用来代指单位正交向量,后来发现不然,一个线性空间可以有无数组基,单位正交向量只是比较特殊的一组基。这种反直觉让我当时不舒服了好一会儿,后来有次蹲坑忘带手机被迫面朝手纸思考人生时,我顿悟了,其实我最开始的感觉并不算错,实际上无数组基分别代表无数个坐标系,每组基向量在对应坐标系里确实是独一无二的,且完全对等于规范正交基在标准坐标系里的地位——也就是说虽然一组基可能长得歪三扭四,但在人家自己的参考系里,人家也是货真价实的“单位正交向量”。上述叙述除了有助于理解基向量外,还表达了一个重要的关窍,即标准坐标系一点都不特殊。
- 线形无关的几何理解:每个向量都给张成的空间增添了一个新的维度。
- 线性相关的几何理解:如果移除某向量组中一部分向量,而不减小该向量组张成空间的维度,即线性相关。
线性变换
- 线性变换定义:线性空间 $V$ 到自身的线性映射。
性质:变换不改变线性关系。
作用对象:向量。 - 理解变换:
- 变换本质上是一种函数,只不过其输入输出对象是向量。使用“变换”而非“函数”,暗示了一种特定的输入输出关系,一般可使用“运动”来理解这种特定关系。但需注意这个运动是瞬时完成的,更像是跃迁,所以从这个角度来讲,变换翻译的非常贴切。
- 变换可以理解为从一个坐标系到另一个坐标系的变换,在转换过程中,整个空间的向量都随坐标系变换而变换。
- 以二维线性空间为例,首先将向量简化为向量终点。接着为了更好地显示整个空间形状的变化,在二维平面上绘制无限方格线,将方格线所有交点视为不同向量的终点。最后对所有向量(交点)同时做变换。这时网格线的变化可以很好地显示整个二维线性空间的形状变化,或者说坐标系变化。
- 理解线性变换(附五种常见线性变换图片演示):
$\Longleftrightarrow$ 任意直线经变换仍为直线,且原点经变换位置不变
$\Longleftrightarrow$ 保持网格线平行且等距分布的变换(横纵分别等距即可,不需要横纵相互等距)
$\Longleftrightarrow$ 说人话:以二维空间为例,只对该空间进行放大缩小旋转等操作,而不对该空间进行弯曲的变换,即线性变换。
矩阵降世
- 由上文可知,变换即坐标系变换。但坐标系太大描述起来不方便,考虑到每个坐标系可由对应的一组基描述,故描述变换可简化为描述一组基的变换。简化的目的不在于丢弃,而是为了提炼一条简明的逻辑,有了这条逻辑我们就可以计算任意向量经变换的位置。接下来我们需要解决两个问题:
第一,如何找到那个描述基向量变换的简洁逻辑?
第二,如何根据基向量的变换计算任意向量经变换的位置?
注:下文中所有 $\vec{v},\vec{i},\vec{j}$ 均指变换前向量,$\vec{v_1},\vec{i_1},\vec{j_1}$ 均指变换后向量。 - 第一个问题,如何找到那个描述基向量变换的简洁逻辑?
- 描述一组基的变换,直观上好像需要描述一组基的初始状态和目标状态。所以我们假设初始状态是规范正交基 $\vec{i}=(1,0),\vec{j}=(0,1)$。那么只需已知规范正交基 $\vec{i},\vec{j}$ 在某变换后的位置 $\vec{i_1}=(a,b),\vec{j_1}=(c,d)$ 即可。
- 需要注意的是,变换后的基向量坐标 $\vec{i_1}=(a,b),\vec{j_1}=(c,d)$ 实际上是在标准坐标系里的坐标,或者说在规范正交基下的坐标。毕竟要是在基向量自家坐标系里,坐标永远都是 $(1,0),(0,1)$ 嘛,这么搞前后坐标都没变还怎么描述变换……故易知,描述基向量变换本质上是在描述一种相对位移。
- 重点来了,之前假设初始状态是规范正交基 $(1,0),(0,1)$,这个 $(1,0),(0,1)$ 本质上是规范正交基在自家标准坐标系里的坐标,那么问题来了,哪组基向量在自家坐标系里不是 $(1,0),(0,1)$?就算我们选组歪瓜裂枣的基向量当初始状态也无所谓,因为目标状态的世界基石是初始状态坐标系而非标准坐标系,就算再歪瓜裂枣人家在初始状态眼里也是 $(1,0),(0,1)$。因此,我们可以愉快地把初始状态直接扔了,留下目标状态,也即新基在旧基下的坐标即可。至于旧基是什么玩意无所谓,注意不要以人类视角理解旧基,可以共情一下新基视角,将旧基视为异世界标准坐标系。
- 综上所述,只需已知新基在旧基下的坐标,即可描述一组基向量的变换。
- 第二个问题,如何根据基向量的变换计算任意向量经变换的位置
- 计算向量变换,首先需要明确向量坐标,我们不能一直躺在标准坐标系的摇篮里不出来。下面给出向量在某组基下坐标的定义:设 $\alpha_1,\alpha_2…\alpha_n$ 为向量空间一组基,则该向量空间中任意向量 $\vec{v}$ 均可被这组基唯一线性表出为 $\vec{v}=\lambda_1\alpha_1+\lambda_2\alpha_2+…+\lambda_n\alpha_n$,其中 $(\lambda_1,\lambda_2…\lambda_n)$ 即向量 $\vec{v}$ 在这组基下的坐标。
- 观察 $(\lambda_1,\lambda_2…\lambda_n)$ 与 $\vec{v}=\lambda_1\alpha_1+\lambda_2\alpha_2+…+\lambda_n\alpha_n$ 易得,向量在某组基下的坐标,等价于向量在对应坐标系下坐标,等价于向量被该组基表出的线性关系。这点不难理解,毕竟上文啰嗦了那么久。
- 已知向量坐标 $(x,y)$ 隐含所在基的线性关系,且变换不改变线性关系,易得:$$\begin{cases}\vec{v}=x\cdot\vec{i}+y\cdot\vec{j}\\\vec{v_1}=x\cdot\vec{i_1}+y\cdot\vec{j_1}\end{cases}$$于是第二个问题轻松解决了,答案即 $\vec{v_1}$,如果将 $\vec{v_1}$ 的坐标写作新基下坐标:$$\begin{equation}\begin{split}\vec{v_1}&=x\cdot\vec{i_1}+y\cdot\vec{j_1}\\&=x\cdot(1,0)+y\cdot(0,1)\\&=(x,y)\end{split}\end{equation}$$咦?坐标没变?没变就对了,这叫变换的坐标不变性,就像你无论怎么扭曲一张坐标纸,点 $(x,y)$ 处永远写的都是点 $(x,y)$。但上文提过变换是在描述相对位移,为体现相对性,新向量一般取旧基下坐标,具体方法只需把 $\vec{i_1},\vec{j_1}$ 取旧基下的坐标,即可算出新向量在旧基下坐标:$$\begin{equation}\begin{split}\vec{v_1}&=x\cdot\vec{i_1}+y\cdot\vec{j_1}\\&=x\cdot(a,b)+y\cdot(c,d)\\&=(ax+cy,bx+dy)\end{split}\end{equation}$$
- 由上文可以得出一个结论,任意二维线性变换仅由四个数字便可完全描述。因此奉天承运,矩阵粉墨登场,让我们引入下列矩阵来描述该线性变换的过程并且山呼万岁吧:$$\begin{bmatrix}a&c\\b&d\end{bmatrix}$$
矩阵
- 用矩阵形式来描述任意向量经某变换后的位置,即:$$\begin{bmatrix}a&c\\b&d\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=x\begin{bmatrix}a\\b\end{bmatrix}+y\begin{bmatrix}c\\d\end{bmatrix}=\begin{bmatrix}ax+cy\\bx+dy\end{bmatrix}$$该矩阵与向量乘法的意义可参考矩阵出生记录,将其理解为新基的线性组合即可。
- 由上条,若将 $(x,y)^T$ 视为基向量之一,则又可得到矩阵与矩阵乘法的意义。$$\begin{bmatrix}a&c\\b&d\end{bmatrix}\begin{bmatrix}x_1&x_2\\y_1&y_2\end{bmatrix}=\begin{bmatrix}ax_1+cy_1&ax_2+cy_2\\bx_1+dy_1&bx_1+dy_2\end{bmatrix}$$上式可理解为两个线性变换的叠加,其中积矩阵的变换效应等价于两者的叠加变换效应,而 $(ax_1+cy_1,bx_1+dy_1)^T,(ax_2+cy_2,bx_2+dy_2)^T$ 可视为经叠加变换后的新基。
PS:不管叠加多少个,等式左右所有矩阵均以最初的异世界标准坐标系为基。 - 这时再回想起矩阵乘法需要从右往左读的奇怪规定,就不难理解了,就是基向量之一先移动到 $(x_1,y_1)$ 再移动到 $(ax_1+cy_1,bx_1+dy_1)^T$。另一种理解是将矩阵当作一种函数,那么矩阵的复合其实就相当于 $f(g(x))$——三蓝一棕酷毙了。至于其他的矩阵运算法则自然也不必多说,呵,现在这些法则全都不配占用我们的海马体了。
- 讲到这里,其实很多矩阵相关的概念猜都能猜明白了,下面简单写写。
- 比如逆矩阵,不就是唱着倒带从哪来往哪去嘛。那么逆矩阵的定义 $AA^{-1}=E$,就代表着这两个矩阵相乘会得到一个“什么都不做”的矩阵,即单位矩阵。
- 正交矩阵也很简单,代表组成矩阵的列向量组是一组“规范正交基”,当然,不仅仅是我们标准参考系里的规范正交基。
- 矩阵的秩则指经变换后空间的维数,或指矩阵的列向量张成的空间维数。若不满秩则意味着变换使空间发生了压缩。维度压缩会带来一个小小的后果,那就是这个变换不再可逆,因为在压缩的过程中,消失方向上的信息丢失了。
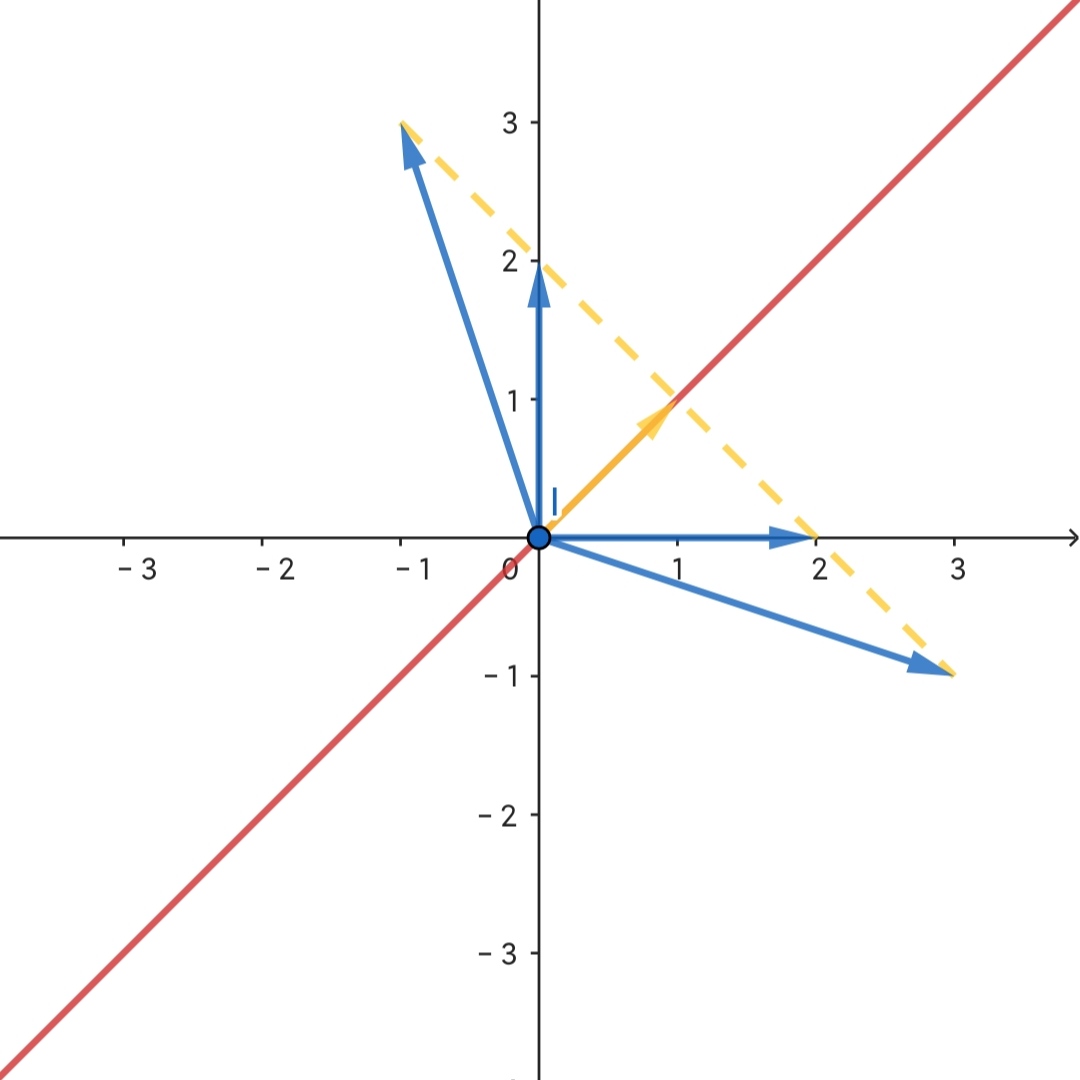 如图所示,该变换矩阵为 $\begin{bmatrix}1&1\\1&1\end{bmatrix}$,意味着整个二维空间被压缩到了红线上。故所有终点在橙色虚线上的蓝色向量,也都随之被压缩到黄色向量上。那么问题来了,如果你知道黄色向量,你能还原出所有蓝色向量吗?显然不能,函数的一个输入对应多个输出那还得了?
如图所示,该变换矩阵为 $\begin{bmatrix}1&1\\1&1\end{bmatrix}$,意味着整个二维空间被压缩到了红线上。故所有终点在橙色虚线上的蓝色向量,也都随之被压缩到黄色向量上。那么问题来了,如果你知道黄色向量,你能还原出所有蓝色向量吗?显然不能,函数的一个输入对应多个输出那还得了? - 我没想到的是,在学习过程中定义看起来最无脑的转置矩阵,涉及的内容竟然是踏马最复杂的!我粗略了解了一下,好像涉及到对偶空间变换,有时间我必然去学习一下,我保证。
行列式
- 提问:请问如何测量一个变换对空间拉伸或压缩的比例?
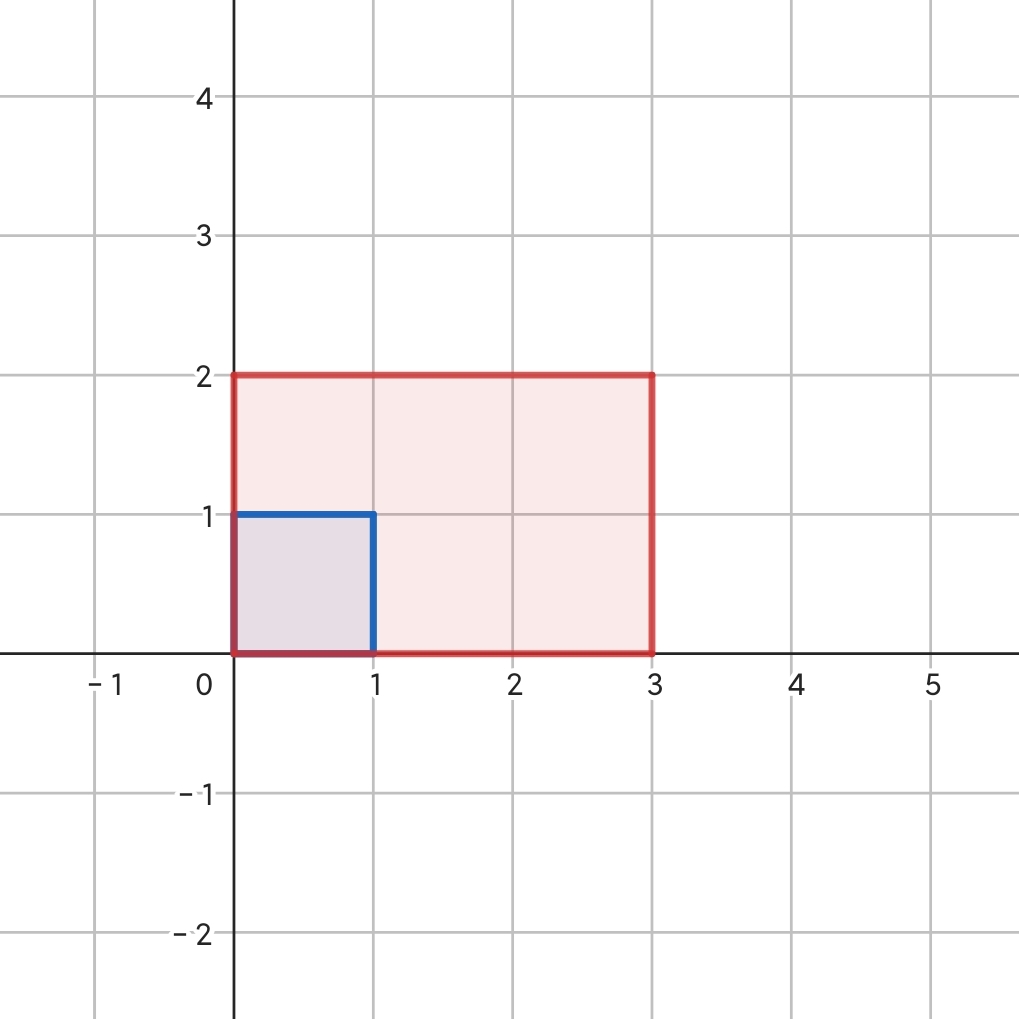
答案:求该变换的行列式,下面举例说明。 - 对于矩阵 $\begin{bmatrix}3&0\\0&2\end{bmatrix}$,由下图易知,该变换将 $\vec{i}$ 拉伸了三倍,将 $\vec{j}$ 拉伸了两倍,将空间拉伸了 6 倍。故该行列式的值为 $3\times2=6$。由此可见,行列式主对角线反映的是基向量在各自坐标轴上的放缩比例。
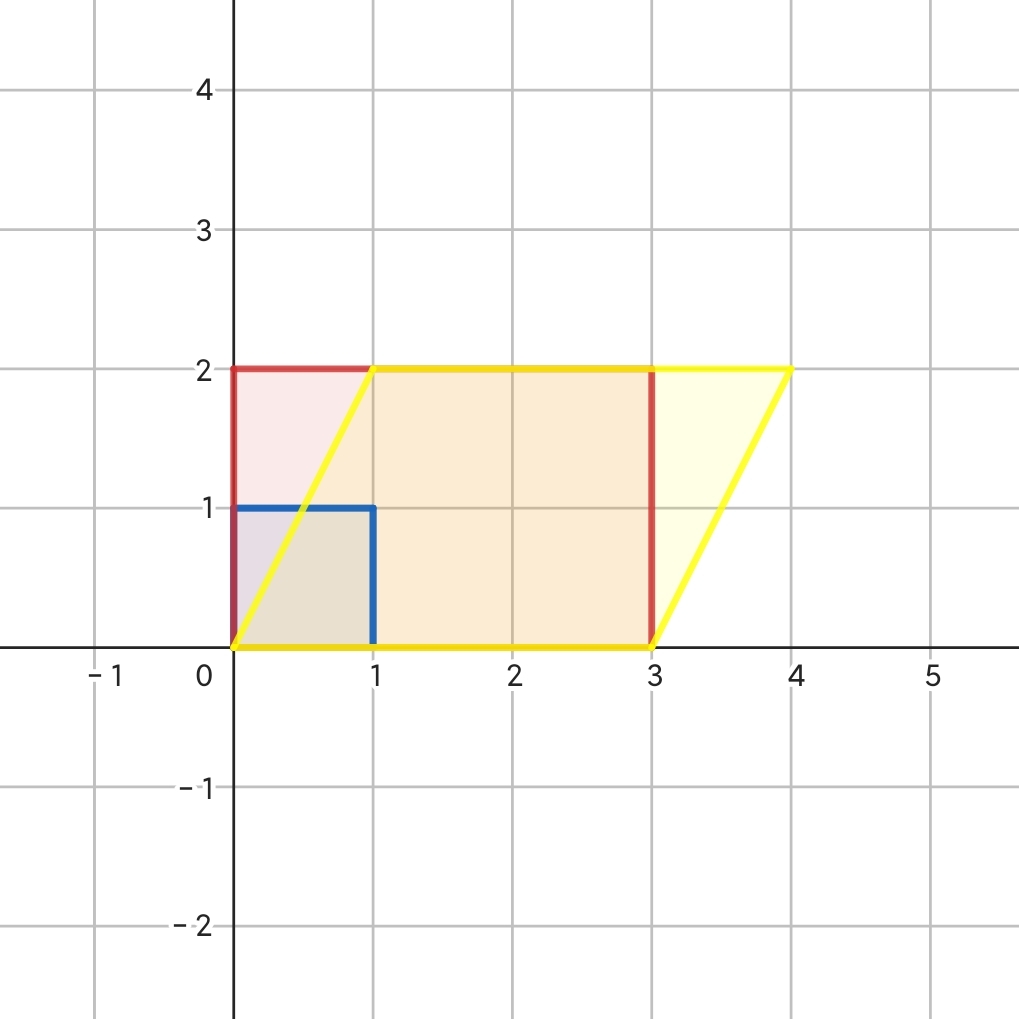
- 对于矩阵 $\begin{bmatrix}3&1\\0&2\end{bmatrix}$,该行列式副对角线只有一个是零,由下图黄色部分易知,该变换呈平行四边形,但仍将空间拉伸了 6 倍。故该行列式的值仍为 $3\times2-0=6$。
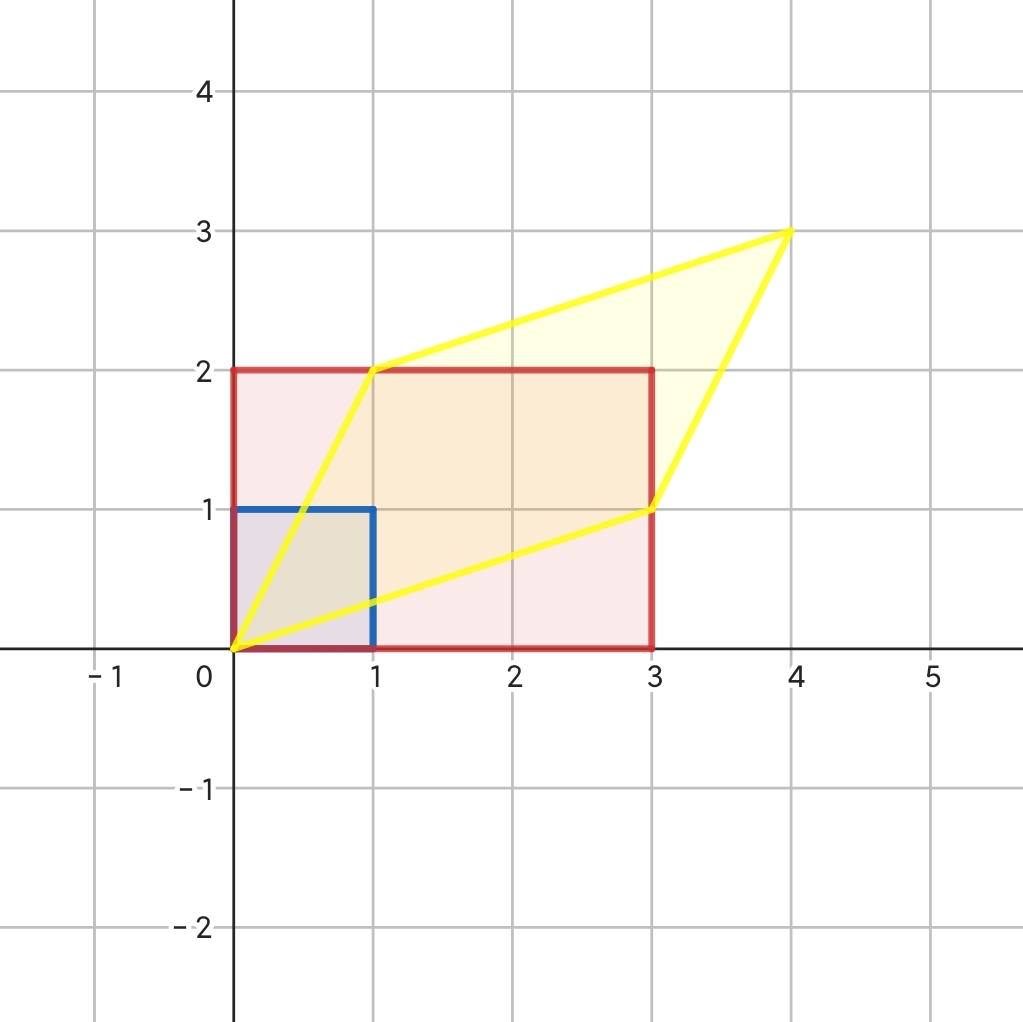
- 对于矩阵 $\begin{bmatrix}3&1\\1&2\end{bmatrix}$,该行列式副对角线均不为零,由下图黄色部分易知,该变换对平行四边形的对角方向进行了压缩,用瞪眼观察法很容易求出黄色部分面积,可知压缩的比例正好为副对角线之积,故该行列式的值仍为 $3\times2-1\times1=6$。
- 行列式出现负值,意味着该变换改变了空间的定向。以二维空间为例,想象 $\vec{j}$ 像时钟指针一样靠近并转过 $\vec{i}$ 的过程中,空间会被逐渐压缩至零然后再次拉伸增大,就像你在现实世界逐渐翻过一张纸片,那么行列式的值先减小至零后继续减小至负值是一件很自然的事情。至于三维空间判断方向需要用右手定则,其余均同理。
- 行列式为零,代表变换减小了该空间的维度。比如使二维平面压缩成线或点,那么变换后的空间面积为0,使三维空间压缩成面、线、点,那么变换后的空间体积为0。
线性方程组
- 说到方程组,我们可能会想到形式五花缭乱的一堆例子,这些例子很难用同一种方式处理。但对于某些特定形式的方程组,比如未知数系数均为常数且未知数之间只进行加法运算的方程组,则可用线代的方式统一处理,我们称之为线性方程组。$$\begin{cases}a_1x_1+b_1x_2+c_1x_3=d_1\\a_2x_1+b_2x_2+c_2x_3=d_2\\a_3x_1+b_3x_2+c_3x_3=d_3\end{cases}$$经过线代半年的摧残,显然这个方程组跟矩阵与向量乘法长得很像:$$\begin{bmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}=\begin{bmatrix}d_1\\d_2\\d_3\end{bmatrix}$$我们将上述方程组记为 $A\vec{x}=\vec{d}$。
- 但有了上文的啰嗦,这种 $A\vec{x}=\vec{d}$ 在我们眼里已经不仅仅是简化方程组书写这点作用了,它还揭示了求解线性方程组的几何意义——即寻找一个向量 $\vec{x}$ 使其在变换后能与向量 $\vec{d}$ 重合。由上文对逆矩阵的理解,也可以理解为 $\vec{x}=A^{-1}\vec{d}$。然后,这么一大坨未知数就被脑海中的空间变换和两条向量取代了,显然非常有益于我们的身心健康。
- 现在考虑系数矩阵不满秩的情况:
- 对于齐次线性方程组,若系数矩阵不满秩,意味着不仅维度发生了压缩,而且解向量在变换后需与零向量重合,即落到原点。
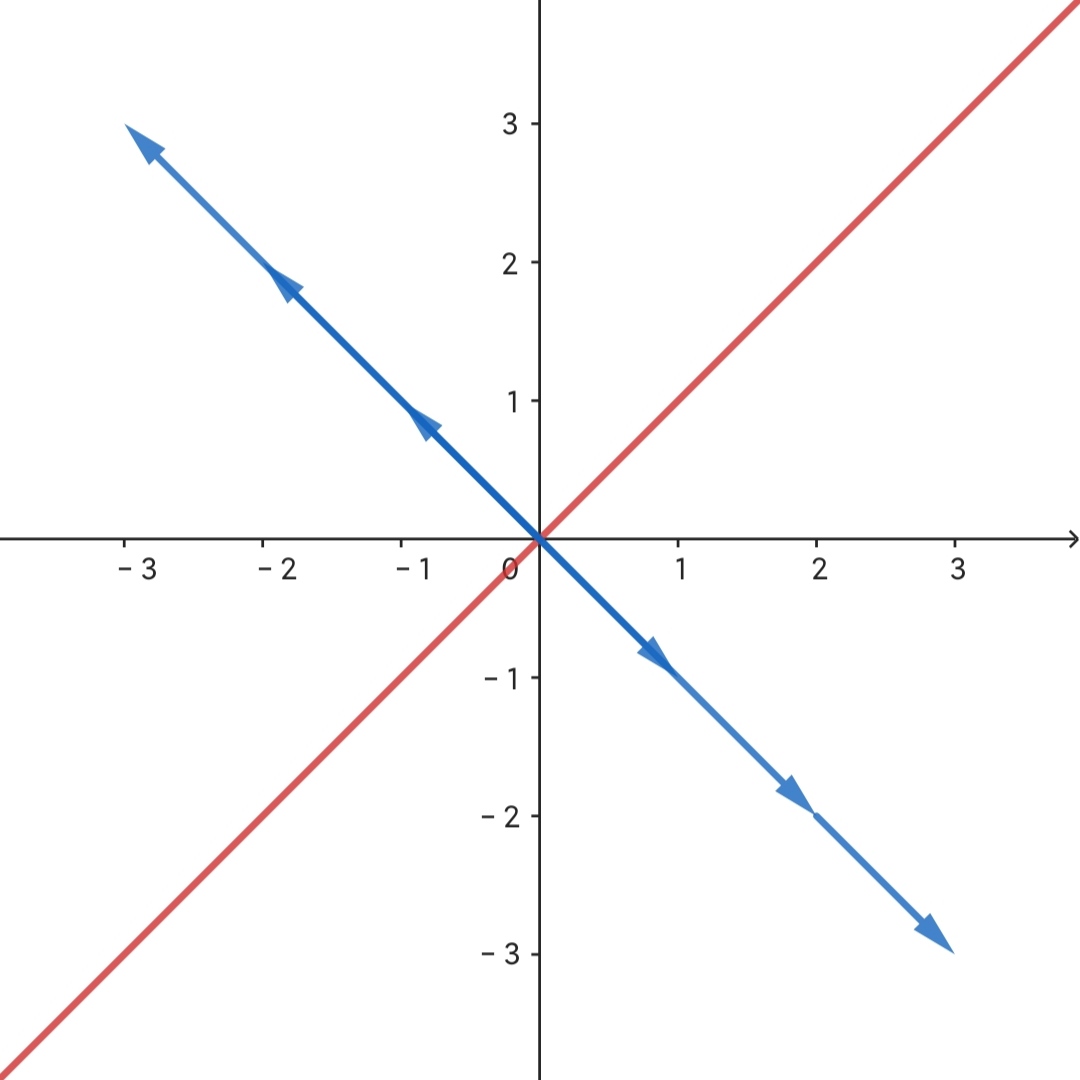 如图所示,系数矩阵为 $\begin{bmatrix}1&1\\1&1\end{bmatrix}$,故整个二维空间被压缩到红线上,所有蓝色向量均被压缩至原点。那么容易看出所有蓝色向量均为解向量,又称基础解系或者解空间。
如图所示,系数矩阵为 $\begin{bmatrix}1&1\\1&1\end{bmatrix}$,故整个二维空间被压缩到红线上,所有蓝色向量均被压缩至原点。那么容易看出所有蓝色向量均为解向量,又称基础解系或者解空间。 - 非齐次线性方程组的道理很相似,唯一的区别是常数项不全为 0,故解向量变换后需与常数列向量重合。
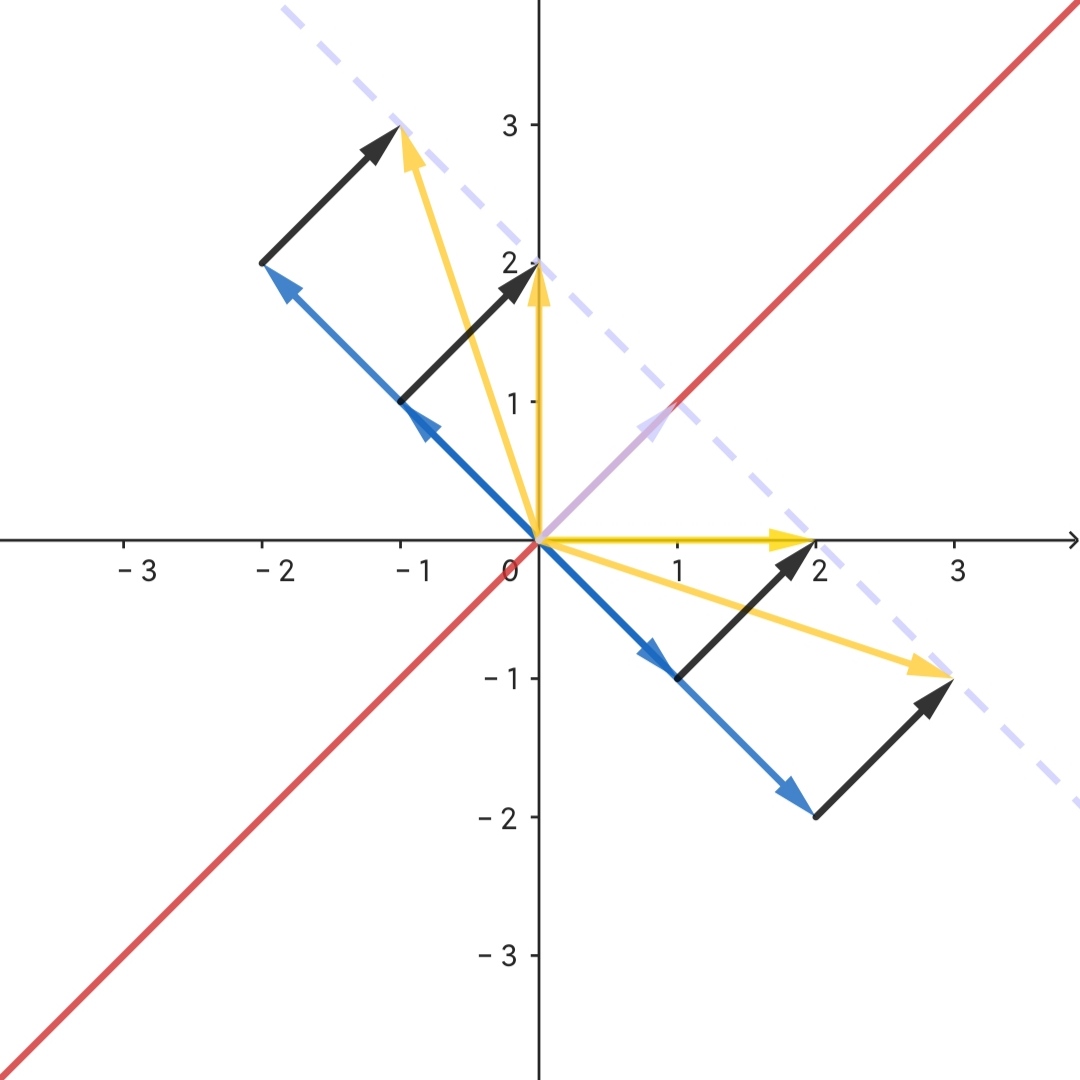 如图所示,系数矩阵仍为 $\begin{bmatrix}1&1\\1&1\end{bmatrix}$,常数列向量为 $(1,1)^T$,故所有橙色向量均被压缩至青色向量。容易看出,每一个橙色向量均为黑色向量和蓝色向量相加而得,显然,黑色向量即为非齐次线性方程组的特解,蓝色向量即为对应齐次方程组的基础解系。
如图所示,系数矩阵仍为 $\begin{bmatrix}1&1\\1&1\end{bmatrix}$,常数列向量为 $(1,1)^T$,故所有橙色向量均被压缩至青色向量。容易看出,每一个橙色向量均为黑色向量和蓝色向量相加而得,显然,黑色向量即为非齐次线性方程组的特解,蓝色向量即为对应齐次方程组的基础解系。 - 此外我们很容易想象,为什么基础解系的个数是 $n-r$:
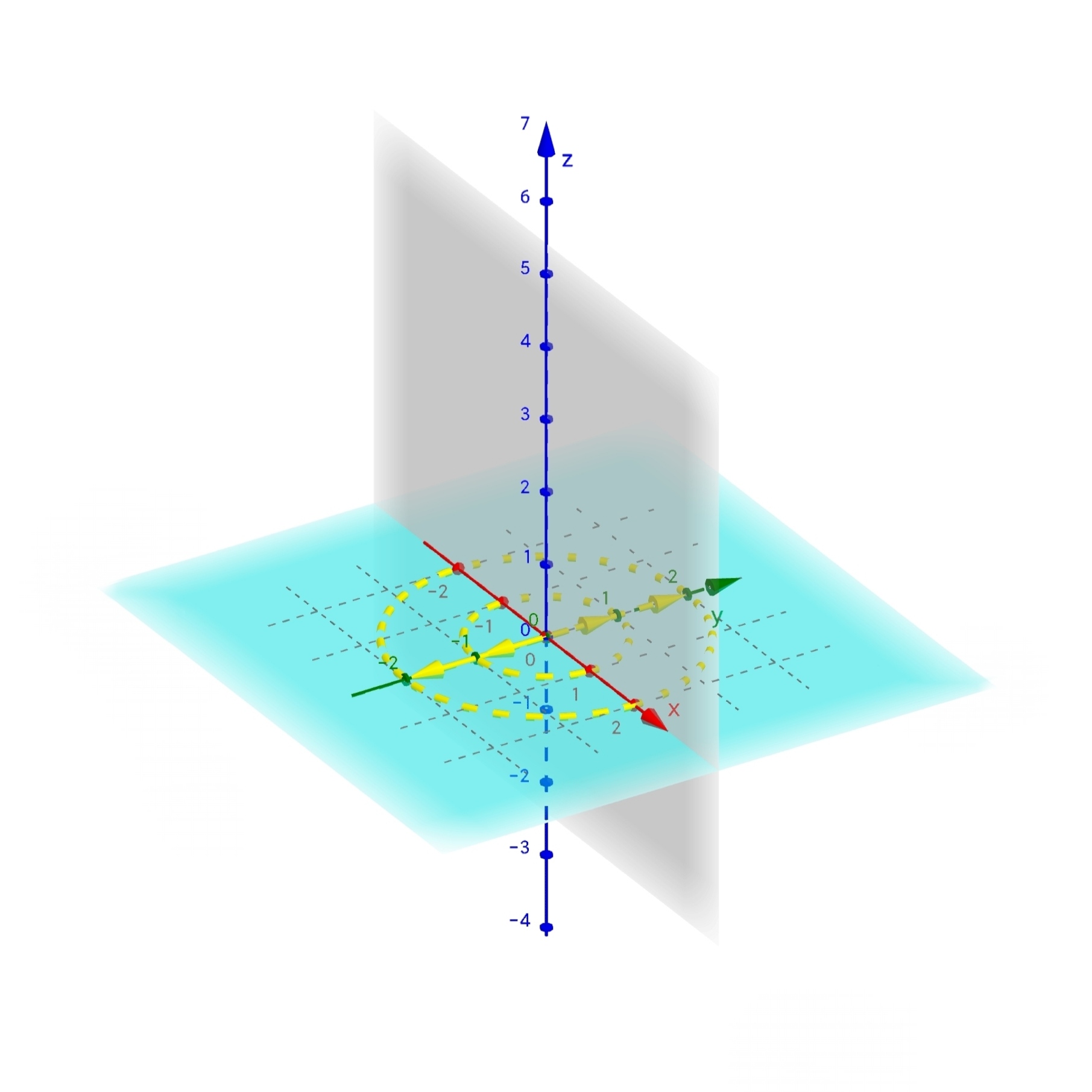 如图所示,当空间压缩到到灰色平面上时,解空间为黄色向量所在直线;当空间压缩到 z 轴上时,解空间为黄色虚线所在平面。所以我个人认为,可以把解空间理解为被压缩维度构成的空间。
如图所示,当空间压缩到到灰色平面上时,解空间为黄色向量所在直线;当空间压缩到 z 轴上时,解空间为黄色虚线所在平面。所以我个人认为,可以把解空间理解为被压缩维度构成的空间。 - 下面引入零空间的定义。对于满秩变换,只有零向量会在变换后落到原点,这也是齐次方程组满秩则只有零解的几何意义。但是对于不满秩变换,会有一系列向量在变换后成为零向量。参考上条图示,如果三维变换将空间压缩到一个平面上,则会有一整条直线的向量被压缩到原点。如果三维变换将空间压缩到一条直线上,则会有一整个平面的向量被压缩到原点。我们将变换后落到原点的向量集合,称为矩阵的零空间。噢,也就是说齐次方程组的解空间貌似又多了一个名字…
- 对于齐次线性方程组,若系数矩阵不满秩,意味着不仅维度发生了压缩,而且解向量在变换后需与零向量重合,即落到原点。
相似矩阵
- 在开始本节之前,首先给出更严谨的矩阵定义:矩阵是线性空间中线性变换的一个描述。若选定一组基,则任意线性变换均能够用唯一一个矩阵加以描述。
理解这句话的关键,在于区分“线性变换”与“线性变换的一个描述”。就像面向对象语言里,一个对象可以有多个引用,每个引用可以叫不同的名字,但都指向同一个对象。同样的,对于一个线性变换,只要你选定一组基,就可以找到一个矩阵描述这个线性变换。换一组基,就可以换另外一个矩阵描述。虽然这些矩阵都是同一个线性变换的描述,但它们都不是线性变换本身。那么问题来了,我们怎么判断这个矩阵是不是自己人? - 在处理这个身份认证问题前,先回答另一个问题:
假设选定一组基 $B_1$ 描述某变换,并已知变换矩阵,即变换后的基 $B_2$ 在 $B_1$ 下的坐标。那么请问若用另一组基 $B_{\alpha}$ 描述同一个变换,则变换矩阵,即变换后的基 $B_{\beta}$ 在 $B_{\alpha}$ 下的坐标是什么?
直觉上的答案,把变换矩阵写成 $B_{\alpha}$ 下的坐标不就行了吗?但这么做实际上就像对 $e^x$ 求二阶导,给虚拟机套虚拟机,等于是把 $B_2$ 在 $B_1$ 下的坐标继续写作 $B_{\alpha}$ 下的坐标,说人话就是把 $B_2$ 这组基连换了两个坐标系,就算再换十个这个变换的起止点也还是 $B_1$ 和 $B_2$ 嘛。 - 正确的思路应该是:假设有一个以 $B_{\alpha}$ 为基的向量,先把这个向量转化为 $B_1$ 下的向量,然后对其进行 $B_1$ 到 $B_2$ 的已知变换,最后再转换回 $B_{\alpha}$ 下的向量即可。标准过程如下:
- 设 $B_2$ 在 $B_1$ 下的坐标为 $\begin{bmatrix}0&-1\\1&0\end{bmatrix}$,$B_{\alpha}$ 在 $B_1$ 下的坐标为 $\begin{bmatrix}2&-1\\1&1\end{bmatrix}$,任意向量在 $B_{\alpha}$ 下的坐标为 $(x_{\alpha},y_{\alpha})$。
- 计算 $\begin{bmatrix}2&-1\\1&1\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}$,由坐标不变性,所得结果为向量 $(x_{\alpha},y_{\alpha})$ 在 $B_1$ 下的坐标 $(x_1,y_1)$。
- 计算 $\begin{bmatrix}0&-1\\1&0\end{bmatrix}\begin{bmatrix}2&-1\\1&1\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}$,得向量 $(x_1,y_1)$ 经变换后在 $B_1$ 下的坐标 $(x_2,y_2)$ 。
- 计算 $\begin{bmatrix}2&-1\\1&1\end{bmatrix}^{-1}\begin{bmatrix}0&-1\\1&0\end{bmatrix}\begin{bmatrix}2&-1\\1&1\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}$,将 $(x_2,y_2)$ 再变换回 $B_{\alpha}$ 下的坐标 $(x_{\beta},y_{\beta})$。
- 故对 $B_{\alpha}$ 向量 $(x_{\alpha},y_{\alpha})$ 而言,矩阵 $\begin{bmatrix}2&-1\\1&1\end{bmatrix}^{-1}\begin{bmatrix}0&-1\\1&0\end{bmatrix}\begin{bmatrix}2&-1\\1&1\end{bmatrix}=\begin{bmatrix}1/3&-2/3\\5/3&-1/3\end{bmatrix}$ 等价于原变换矩阵。
- 受过线代摧残的同志们想必已经发现,上述形式即 $\begin{bmatrix}1/3&-2/3\\5/3&-1/3\end{bmatrix}$ 的相似矩阵定义式!
- 对于 $P^{-1}AP\alpha=B\alpha$,有一个对脑子很友好的理解方式,我们可以把 $A$ 矩阵看作已知的变换矩阵,把外侧的 $P$ 与 $P^{-1}$ 反抽象成视角的转换,那么这个式子的意义就很清晰明了了。
- 回到最开始的问题,如果你给我两个矩阵,我怎么知道这两个矩阵是不是描述的同一个线性变换?答案就是判断两个矩阵是否相似:若矩阵 $A$ 与 $B$ 是同一个线性变换的不同描述,则一定存在可逆矩阵 $P$,使得 $A$、$B$ 之间满足这样的关系:$P^{-1}BP=A$。
特征值与特征向量
- 假设任意向量都能张成一个直线空间,那么在很多变换中,几乎所有向量都会离开自己张成的空间,但也有一些特殊的向量仍会留在其中,我们称这些特殊的向量为该变换的特征向量,而特征向量被拉伸或压缩的因数即该特征向量的特征值。可以这么理解,对一个复杂的线性变换,只要找出特征值与特征向量,那么该线性变换就可以看作线性空间在特征向量方向上缩放了一定倍数。
- 这时候回忆一下曾经莫名其妙的特征值和特征向量定义:若 $A\alpha=\lambda\alpha$,则 $\alpha$ 为变换矩阵 $A$ 的特征向量,$\lambda$ 为 $\alpha$ 对应的特征值。是不是有种一览无余的感觉?
- 下面是具体计算和一些性质:
- 由于 $A\alpha=\lambda\alpha$ 左侧是矩阵向量乘法,右侧是向量数乘。于是我们首先将右侧也改造为矩阵向量乘法,其中矩阵的作用效果应为将任意向量乘 $\lambda$,显然该矩阵型为 $\begin{bmatrix}\lambda&\\&\lambda\end{bmatrix}$。那么 $A\alpha=\lambda\alpha$ 便可转化为 $(A-\lambda E)\alpha=0$。And bingo,现在求解特征值与特征向量被我们成功搞成求解齐次线性方程组了。
- 同一个特征值对应的特征向量不一定只有一个。比如二维线性空间中将一组基分别拉长三倍,那么空间中所有非零向量均为特征值 3 的特征向量。或者错切变换,空间中只有 x 轴上的向量为特征值 1 的特征向量。

- 不同特征值对应的特征向量线性无关。这点现在很好理解,如果线性相关,那么缩放的倍数必然一致,与特征值不同矛盾,证毕。
- 相似对角化。
- 若某变换矩阵的特征向量恰为变换前参考系的基,那么说明此线性变换仅对坐标轴进行了缩放,且变换矩阵必然为对角矩阵。而对角矩阵有多迷人就不必多说了。一个联系很紧密的好处就是,矩阵对角元即特征值,矩阵列向量即特征向量。
- 当然了矩阵特征向量正好是基向量的情况还是很少见的。但是为了得到迷人的对角矩阵,我们可以强行让特征向量作为基向量——当然了想强行登基也得有那潜力,而这就是相似对角化充要条件的根源,即 n 阶矩阵须有 n 个线性无关特征向量,只有这样,特征向量才能张成维度足够的空间。
- 接下来的过程我们用正常人语言描述:对于任意向量,我们从登基后视角换到 $A$ 视角 $\longrightarrow$ 用 $A$ 矩阵变换 $\longrightarrow$ 换回登基后视角 $\longrightarrow$ 得到登基视角的变换后向量,用非人类语言即 $P^{-1}AP\alpha=B\alpha$。而其中 $B$ 矩阵必为对角阵,且对角元必为特征值。原因很明显,特征向量登基后,该变换中的基向量就只剩缩放了。
- 最终,我们可以由 $P^{-1}AP=\Lambda$ 得到特征基视角的 $A$ 变换。这种视角转换有很多好处,但对我等做题狗而言,最亲切的是简化矩阵 n 次方计算步骤。我们可以先转换到特征基视角计算对角矩阵 n 次方,然后再转换回原视角即可。
全文暂时完